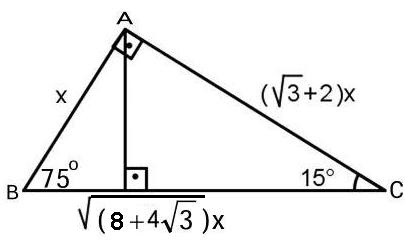
X 12 2x 3 üçgeninde x 5 olursa 5 12 13 üçgeni olur x 5 bulunur 33 ABC üçgen AN açıortay m ABC 45 m ACB 75 AC Yukarıdaki verilere göre, oranı kaçtır? 5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklikParalelkenar Çözümlü Sorular test soruları ve çözümlerinin anlatıldığı dörtgenler çözümlü soruları sayfasıdır x kaç derecedir?

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
15 75 90 üçgeni alan bulma
15 75 90 üçgeni alan bulma-Yukarıdaki 15 75 90 üçgeni özellikleri, bu üçgenlerde kullanılarak sorunun doğru yanıtı bulunur 15 75 90 Üçgeni Kenar Uzunlukları Elimizde bir tane 15 75 90 üçgeni olduğunu hayal edelim ABC üçgeninin açıları şu şekilde olsun A açısı 90° B açısı 75° C açışı 15° Açılar böyleyken 15 75 90 üçgenininDik üçgende dik kenarların uzunluklarının kareleri 15 75 90 Üçgeni Geniş Açı Nedir Sitede yer alan haber ve içeriklerin tüm hakları saklıdır ve buradaki bilgiler sadece bilgilendirme amaçlı olup, kullanımına, uygulanmasına, satın alınmasına, delil gösterilmesine veya tavsiye edilmesine aracılık etmez Sitemizdeki bilgiler, hiç bir zaman kesin bilgi kaynağı olmayıp



Dik Ucgende Trigonometrik Oranlar
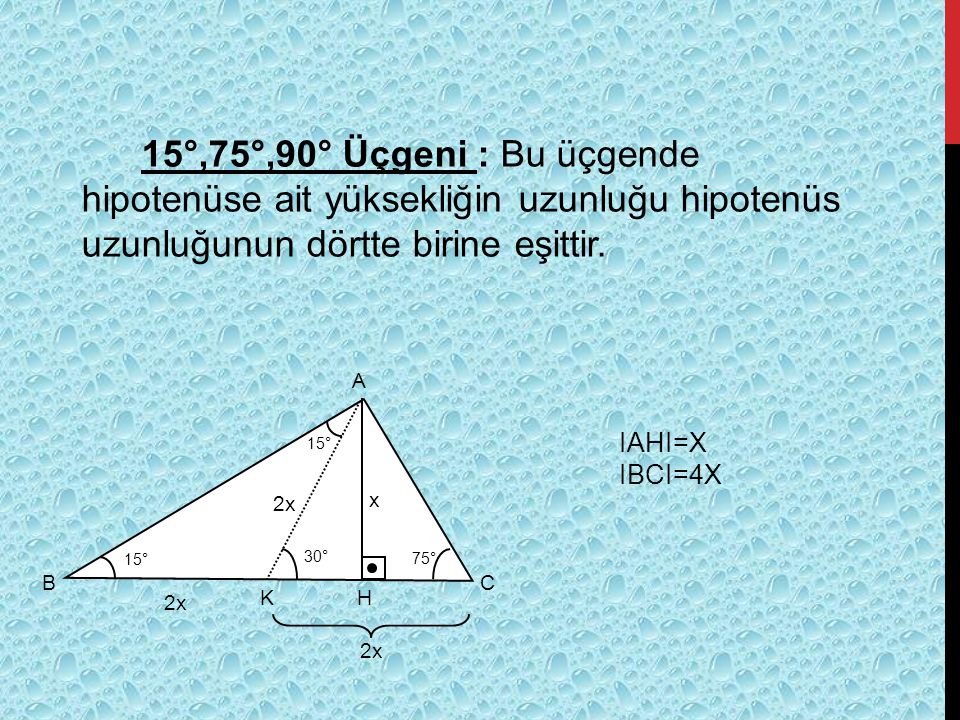
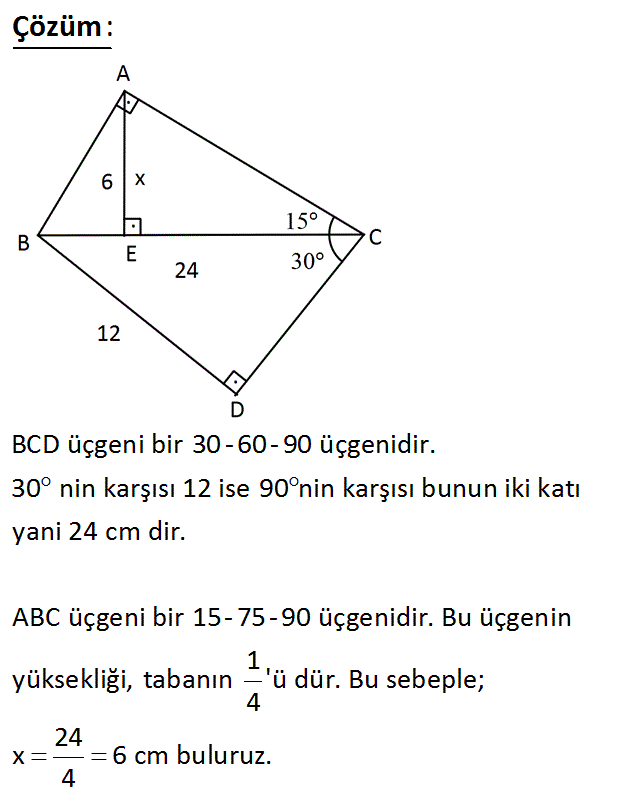
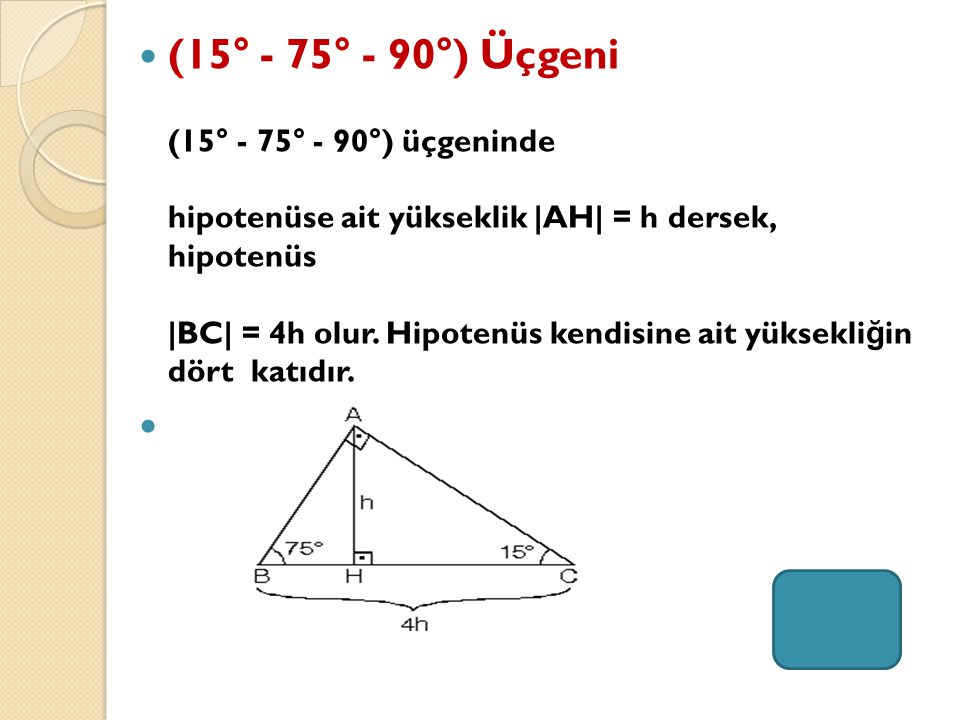
Arkadaşlar bu konumuzda Üçgende Alan Formülleri ve Üçgende Alan Formülü Bağıntılarından bahsedeceğiz Bu formülleri TYT sınavlarınızda da kullanabilirsiniz Özel dik üçgenlerden olan 15 – 75 – 90 üçgeninde dik açıdan indirilen yükseklik, hipotenüs uzunluğunun ¼ 'ne eşittir üçgeni orantılı bir Toplamları 135 olan 15 tane sayma sayısı vardır Bu sayılardan bir kısmının ortalaması 13, diğerlerinin ortalaması 7 dir Bu sayılardan kaç tanesinin ortalaması 7 dir 2 ve 9 ile bölünebilen pozitif Bir tam sayının tam olarak 15 tane pozitif böleni varsa bu sayının 5 ile bölümünden kalan kaç olurDairede Alan (İSPAT) Üçgeni Kenar Bağıntısı ( İSPAT ) Heronİç teğet çember arasındaki güzel bir ilişki;
Bunun yerine tüm kenarları toplayarak da çevre uzunluğunu bulabilirdik Refleks 2 30° 60° 90° Üçgeni 559 Refleks 3 30° 30° 1° Üçgeni 432 Refleks 4 15° 75° 90° Üçgeni 645 Refleks 5 22,5° 67,5° 90° Üçgeni 549 Refleks 6 Küçük Üçgenden Yola Çıkarak Büyük Üçgeni Tamamlama 31217 Ocak 12 16 Ocak 12 xMaTeMaTiK 0 yorum (15° 75° 90°) Üçgeni, (3 4 5) Üçgeni, (30° 30° 1°) Üçgeni, (30° – 60° – 90°) Üçgeni, (5 12 13) Üçgeni, İkizkenar dik üçgen, İKİZKENAR ÜÇGENI, ÖKLİT BAĞINTILAR, Üçgenlerde Uzunluk (3, 4, 5) (4, 3, 5) (5, 12, 13) (6, 8, 10) (7, 24, 25) (8, 6, 10) (8, 15, 17) (9, 12, 15) (9, 40, 41) (10, 24, 26) (11, 60, 61) (12, 5, 13) (12, 9, 15) (12, 16,
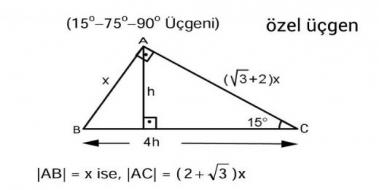
HA x olur HB 2x 3 olur ABH üçgenine bakarsak; Altıgen alan formülü alanını 75 cm 2 bulduysanız ve eksik üçgenin alanını ise 15 cm 2 bulduysanız bu durumda yapmanız gereken 75 – 15 işleminin sonucu hesaplamak ve 60 bulmaktır Geri bildirim 15 75 90 Üçgeni Özellikleri ve Kuralı Öğrenci Yardım Üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu üçgende hipotenüse indirilen dikme, hipotenüsün 1/4 katıdır




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
Bu açı ölçüsü bir üçgeni özel üçgen yapabilmektedir Alan için kenar ve o kenara ait yüksekliğe ihtiyaç duyduğumuza göre dikme inerek soruyu çözelim AB kenarı 6 birim, bu kenara ait dışarıdaki yükseklik de 5 birim bulunur Bu durumda alan 56/2 = 15 br 2 bulunur Aynı soruyu sinüslü alan formülünden de çözebilirizüçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidirÜçgende alan konusu kpss geometri dersi içinde işlenmektedir Kpss sorularında üçgende alan ile ilgili son 12 yılda toplam 8 tane soru çıkmıştır Geometri soruları genel yetenek soruları içinde az bir yer kaplasa da, üçgende alan konusu yıllara göre çıkan soru sayısına göre önemlidir




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com



15 75 90 Ucgeni
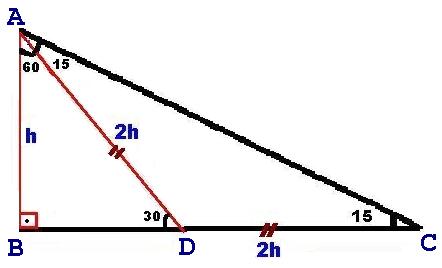
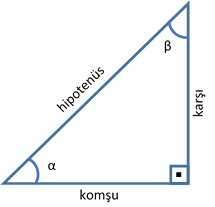
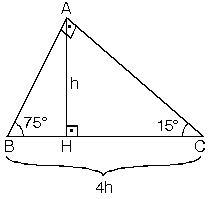
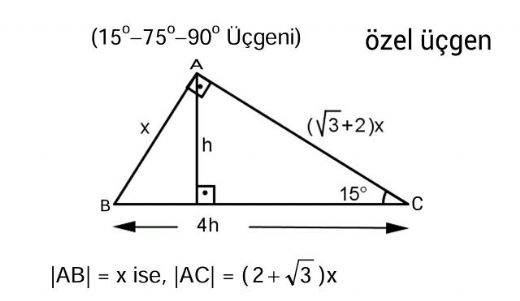
(30 60 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize bekliyoruz ) Tüm Öğrencilerimize İyi Dersler Diliyoruz ) üçgeni Bu üçgende hipotenüsün sahip olduğu yükseklik h olarak kabul edilecek olursa, hipotenüs uzunluğu 4h olur Bir diğer deyişle;Sinüs fonksiyonu karşı kenarın hipotenüse bölünmesidir




15 75 90 Ucgeni Akilli Geometri



Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir
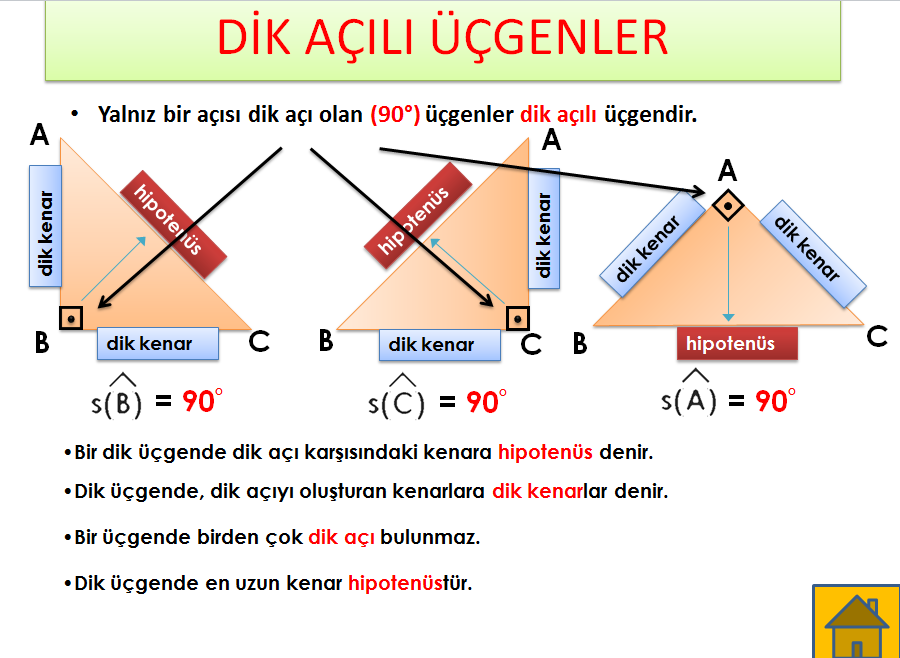
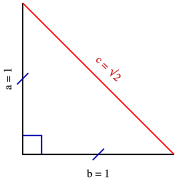
Geometride pek çok üçgen çeşidi bulunmaktadır Dik üçgenler bunlardan birisidir İç açılarından biri 90 derece olan üçgenlere dik üçgen adı verilmektedir Bu nedenle dik üçgenin diğer iki açısının toplamı da 90 derece olmalıdır Bunlar 1575 Yani dik üçgende 30 derecenin karşısında yer alan kenar hipotenüsün yarısı 60 derecenin karşısında yer alan kenar 30 derecedir Bu anlamda karşısında yer alan değerin kare içerisinde üç katıdır üçgeni;Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m (A) = 90° BC kenarı hipotenüs




Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri




Dik Ucgen Vikipedi
17 Ocak 12 16 Ocak 12 xMaTeMaTiK 0 yorum (15° 75° 90°) Üçgeni, (3 4 5) Üçgeni, (30° 30° 1°) Üçgeni, (30° – 60° – 90°) Üçgeni, (5 12 13) Üçgeni, İkizkenar dik üçgen, İKİZKENAR ÜÇGENI, ÖKLİT BAĞINTILAR, Üçgenlerde UzunlukDİK ÜÇGEN 16 15 75 90 ÜÇGENİ Bu Pini ve daha fazlasını Mustafa YAZAGAN tarafından oluşturulan ÜÇGENLER panosunda bulabilirsiniz KişiselStewart Teoremi ( İspat ) Bir Doğrunun



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeni Webders Net
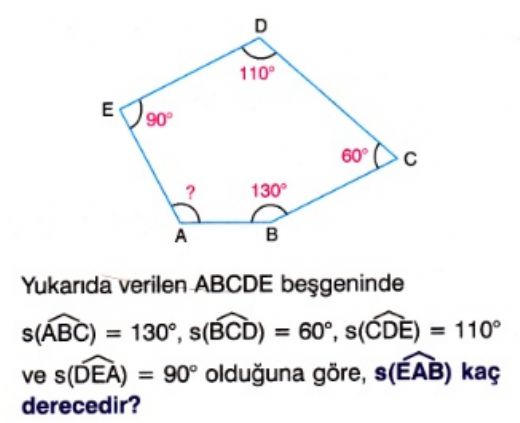
TOPLAM 62 dk Dikdörtgen Refleks 1 Dikdörtgeni TanıyalımAlan = b × c / 2 formülüyle hesaplanır Bir dik üçgen, dikdörtgenin köşeden köşeye kesilmiş halidir Dikdörtgenin alanını hesaplarken kenar uzunluklarını çarparız Bu durumda bu uzunluğu 2'ye bölersek dik üçgeninÇözüm m (ECD)=9024=66 olur




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Matematik Felsefesi Evde Egitim



Ozel Ucgenlerdeki Oranlari Ispatlayiniz 90 75 15 Matematik Kafasi
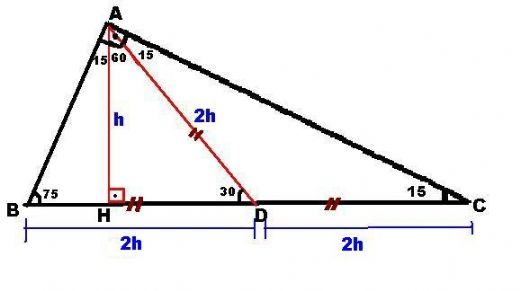
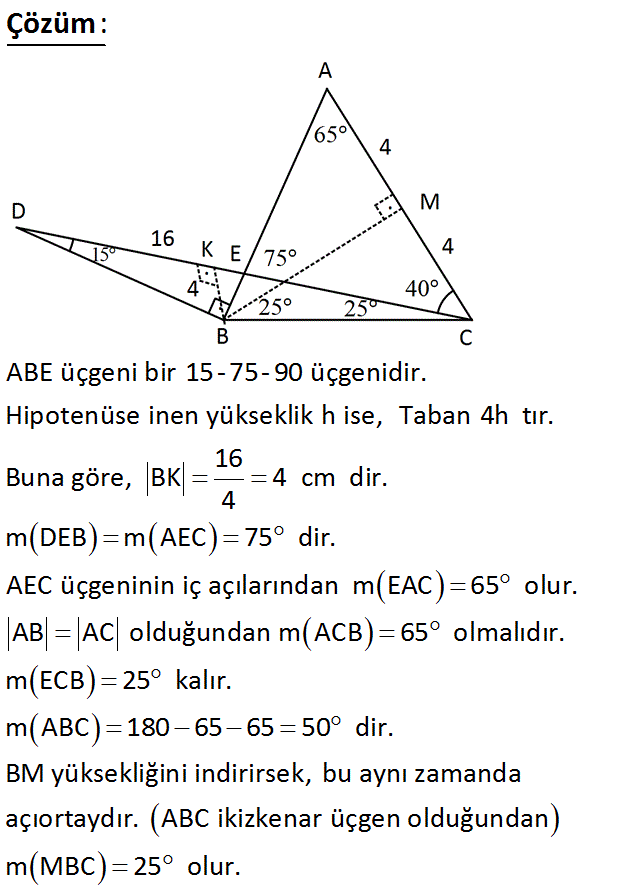
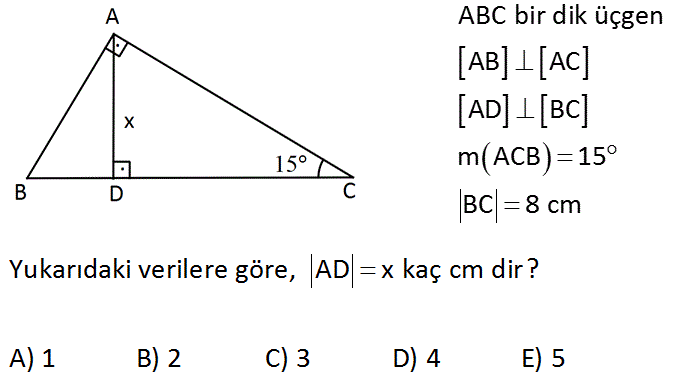
Alan (DEF) = ( DE EF ) ÷ 2 dir Yukarıdaki DEF dik üçgeninin EF dik kenarının uzunluğu 3 birim ve DE dik kenarının uzunluğu 5 birimdir Öyleyse DEF üçgeninin alanı; 5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine aitRefleks 5 22,5°– 67,5°– 90 Refleks 12 Üçgenler Yardımıyla Eşkenar Dörtgende Alan Ve Uzunluk Bulma 647;
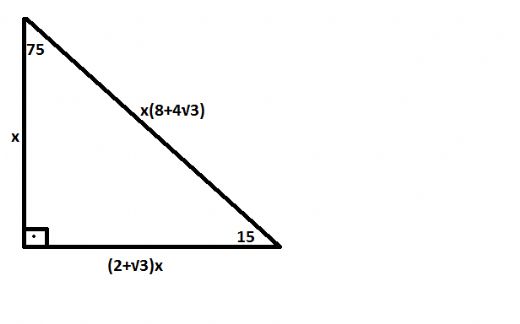



15 75 90 Ucgeninin Ozellikleri Nelerdir



15 75 90 Ucgeni
Geometri dersi, üçgenler konusu İkizkenar dik üçgenler, 30 60 90 üçgeni, 3 4 5 üçgeni, 5 12 13 üçgeni, 8 15 17 üçgeni Konu anlatımı ve örneklerRefleks 4 15°– 75°– 90° Üçgeni 645 Refleks 5 22,5°– 67,5°– 90° Üçgeni 549 Refleks 6 Küçük Üçgenden Yola Çıkarak Büyük Üçgeni Tamamlama 312 Özel üçgenler içinde yer alan dik üçgen, ikizkenar üçgen, eşkenar üçgen kpss geometri konusu anlatımı Üçgeni Bir dik üçgende dar açılardan biri 30 ise, Bir dik üçgende dar açılardan birinin ölçüsü 15 derece ise, hipotenüs uzunluğu hipotenüse ait yüksekliğin 4




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
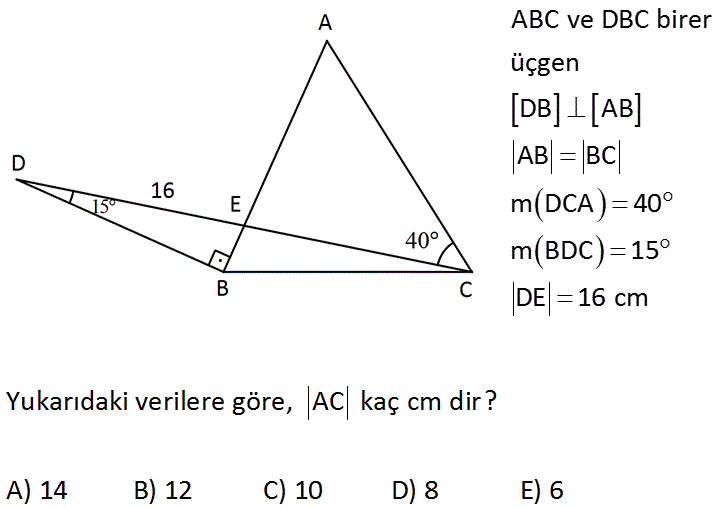
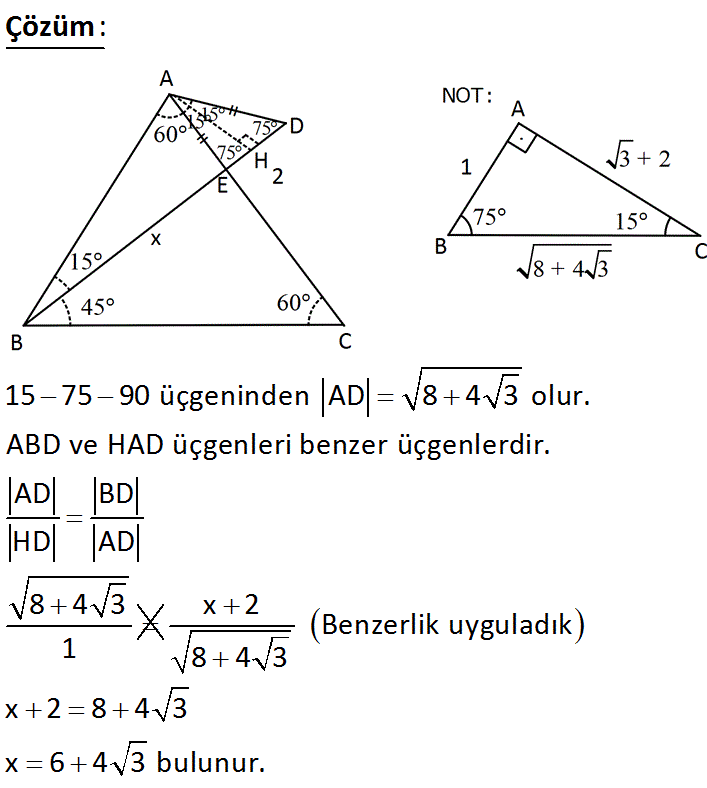
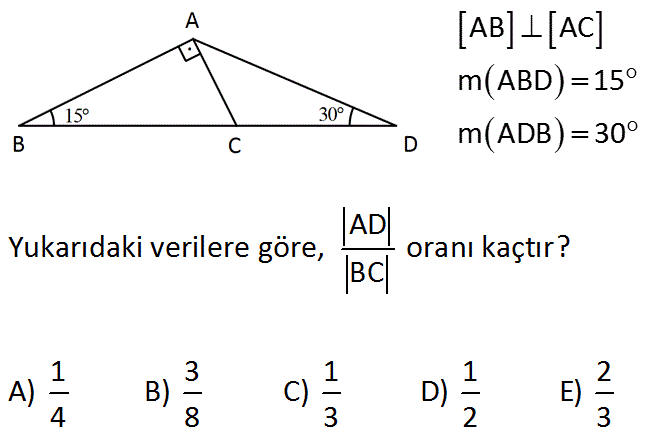
BN A) 1 B) 2 C) 3 D) 2 2 E) 3 Çözüm m (BAC) 180 45 75 180 1 60 dir Açıortay açıları 30 dir N'den D'ye bir dikme (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik cinsinden alan değeri Çemberde Açı Bulma Video Çemberde Açı ve Uzunluk ders notu Çemberde Açı video konu anlatımı Çemberde Uzunluk Bulma Çemberde Uzunluk Püf Noktaları Video Çemberin Analitik İncelenmesi Video Çemberin(15 75 90) Üçgeni (45 45 90) Üçgeni;




15 75 90 Ucgeni Donanimhaber Forum




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
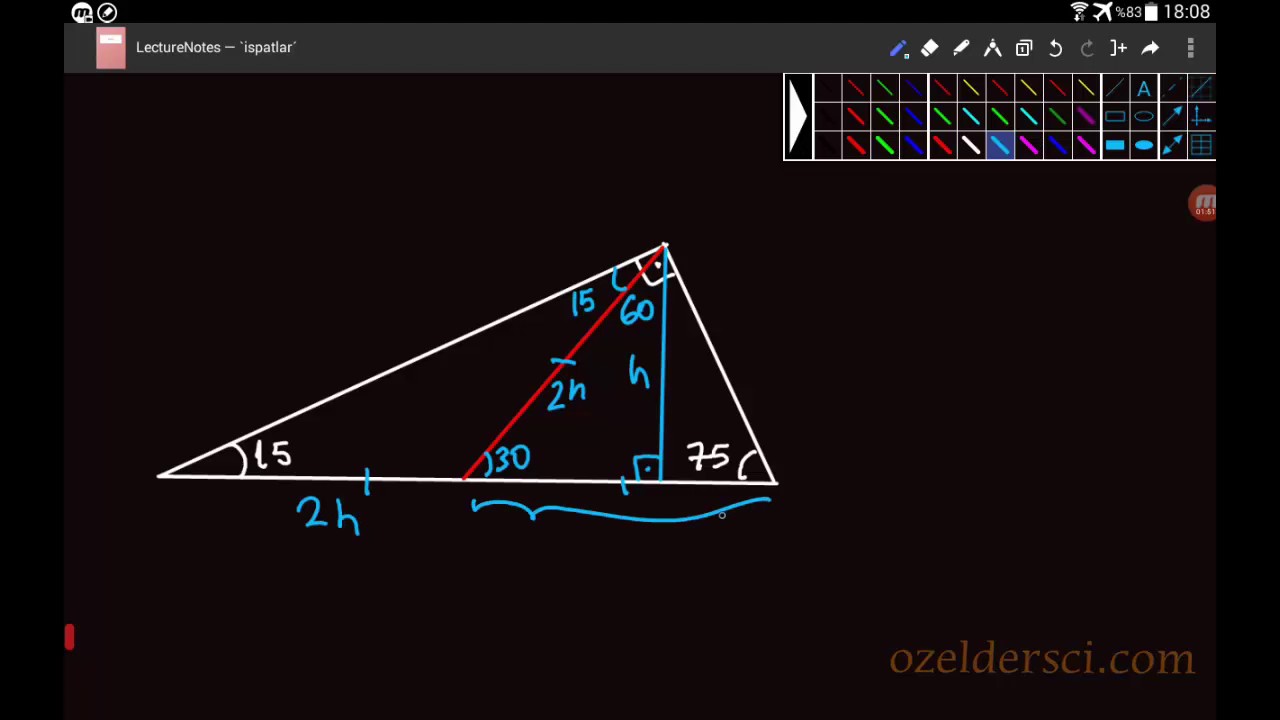
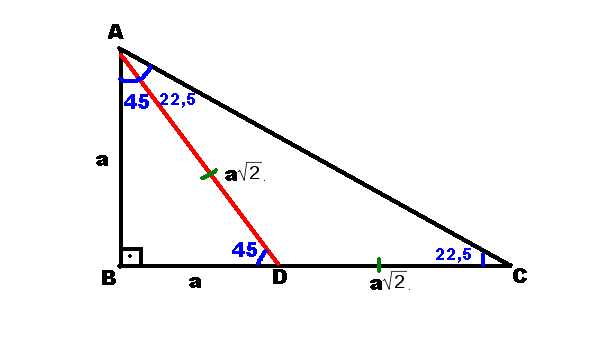
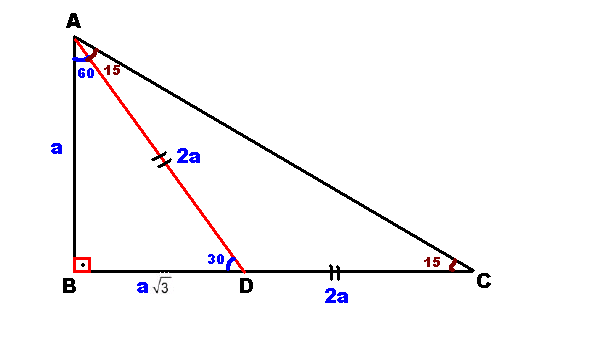
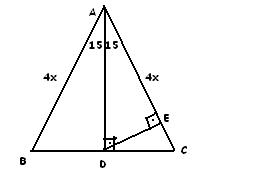
Düzeltme (ben, daha önce, ($\angle OBD=\frac{ 60^{\circ}}2=15^\circ$ olarak düşünüp çözmüşüm!) tepeye ait açıortay tabanı ikiye böler ve üçgeni iki () dik üçgene böler (alan bulma) işlemler o kadar da uzun değilmiş (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in karşısındaki kenar "a" ise 75 in



15 75 90 Ucgeni Webders Net



15 75 90 Ucgeni Ozellikleri
Bir anda oluşan tehlikeli durum Güney amerika'nın en uzun akarsuyu 60'ların efsanevi yeşilçam yıldızı, __ doruk İşlenmiş hayvan postu imalatçısı veya satıcısı Bir arsanın her bir parçası Yat limanı Bulmaca 2 __ denizi, italya ile balkanlar arasındadır Güneşin dünyaya en uzak olduğu an 15 75 90 üçgeni 2 ayrı çözüm yöntemi bulunur bunlardan bir tanesi 75 derecelik açıyı 30 ve 45 olarak, diğeri de 15 ve 60 olarak bölmektir 30 ve 45 olar35=15 15/2=7,5 br2 dir Yandaki KLM üçgeni geniş açılı bir üçgendir Geniş açılı üçgende yükseklik şekildeki gibi çizilebilir




15 75 90 Ozel Ucgeni Oluyor Ama Ben Sadece O Ucgenin Yukseklik Le Ilgili Ozelligini Biliyorum Baska Eodev Com




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu
Üçgeni Kenar Bağıntısı ( İSPAT ) ABC Üçgeninin Alanı = 1/24x4xsin30 olmak üzere 4x²dir ADC Üçgeninin alanı da bunun yarısı 2x²'dir Düzlem geometrisinde yer alan temel şekillerdendir Üçgende üç köşe ve bu üç köşeyi birleştiren kenarlar bulunur Bir üçgenin iç aç 90 75 15 Üçgeni Üçgenin Alanı Dik açılı üçgenin özellikleri nedir?




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com



15 75 90 Ucgeni Ve Ozellikleri
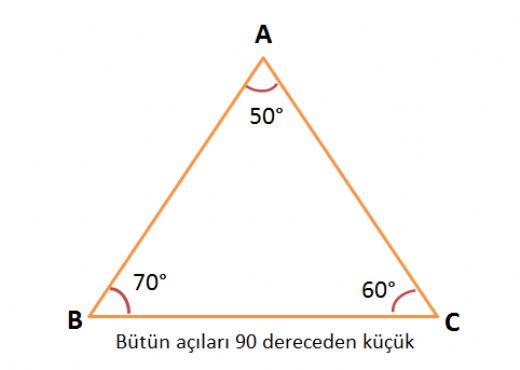
75 i 1560 diye böleceksin O 1515 ikizkenar oluşturacak diğer yerdede oluşacak uzunlukları taşıyacaksın tek tek Karede 15 varsa köşegen çekeceksin köşegenler açıortay olduğu için ve dik kesiştiği için oluşacak Cok basit aslinda bi numarası yok 75 i 1560 diye böleceksinParalelkenarda karşılıklı açılar eşittir 2x40=x10 ise buradan x=50 olur m (ABC) kaç derecedir?Özel Üçgenler DİK ÜÇGEN Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdırşekilde, m(A) = 90° BC kenarı hipotenüs AB ve AC kenarları dik kenarlardır PİSAGOR BAĞINTISI Dik üçgende dik kenarların uzunluklarının




3 4 5 Ucgeni Ve Ozellikleri Not Bu




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List
Refleks 4 15°– 75°– 90° Üçgeni 645;B dik açının komşu kenarlarından bir tanesi, c ise komşu kenarlardan ikincisinin uzunluğu olmak üzere; Üçgenlerinde değişmeyen çevre ve alan formülleri vardır Üçgeni bir araya getiren doğrulara kenar denir Çeşitlerine göre bu kenarların uzunlukları farklılık gösterir 90 75 15 Üçgeni Üçgenin çevresini bulmak ile üçgenin etrafında bulunan mesafeyi bulma aynı anlamlara gelmektedir Bir üçgenin çevresini



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube




Dik Ucgende Trigonometrik Oranlar
Hipotenüs, kendisine ait ola yüksekliğin 4 katıdır




Ikizkenar 15 75 90 Ucgeni Yardim Edebilir Misiniz Cozemedigim Sorular




15 75 90 Ucgeni



15 75 90 Ucgeni




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik




15 75 90 Ucgeni




15 75 90 Ucgeninde H 4h Kuralinin Ispati Youtube




15 75 90 Ozel Ucgeninin Kenar Bagintilari Nedir Eodev Com
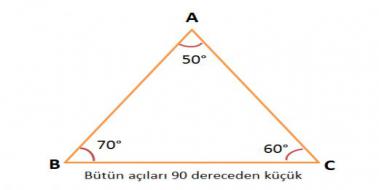



15 75 90 Ucgeni Ozellikleri




15 75 90 Ucgeni Donanimhaber Forum




Bir Ucgenin Alani Nasil Hesaplanir Wikihow
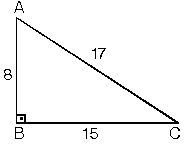



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
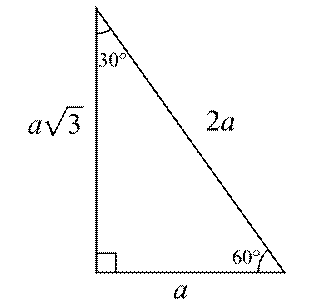



Dik Ucgende Trigonometrik Oranlar
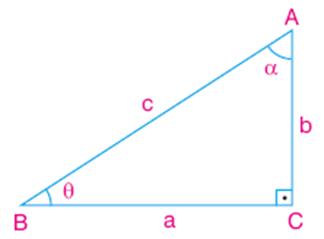



Dik Ucgende Trigonometrik Oranlar




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Alan Ve Kenar Bagintilari Konu Anlatimi



15 75 90 Ucgeni Ozellikleri



Dik Ucgenin Alani Nasil Bulunur Dik Ucgenin Alan Hesaplama Formulu Nedir Son Dakika Egitim Haberleri




選択した画像 75 15 90 Ucgeni Kenarlari



15 75 90 Ucgeni Donanimhaber Forum




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com



15 75 90 Ucgeni




Ucgende Alan Konu Anlatimi Sorulari Cozumleri 9 Sinif Tyt Matematik Ucgenin




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Son Dakika Egitim Haberleri




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz



15 75 90 Ucgeni



45 45 90 Ucgeni Kurali Nedir 45 45 90 Ucgeninin Ozellikleri Nelerdir En Son Haberler




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube



15 75 90 Ucgeni Donanimhaber Forum Sayfa 2



Dik Ucgende Trigonometrik Hesaplamalar



22 5 67 5 90 Ucgeni 1 2 Ispat
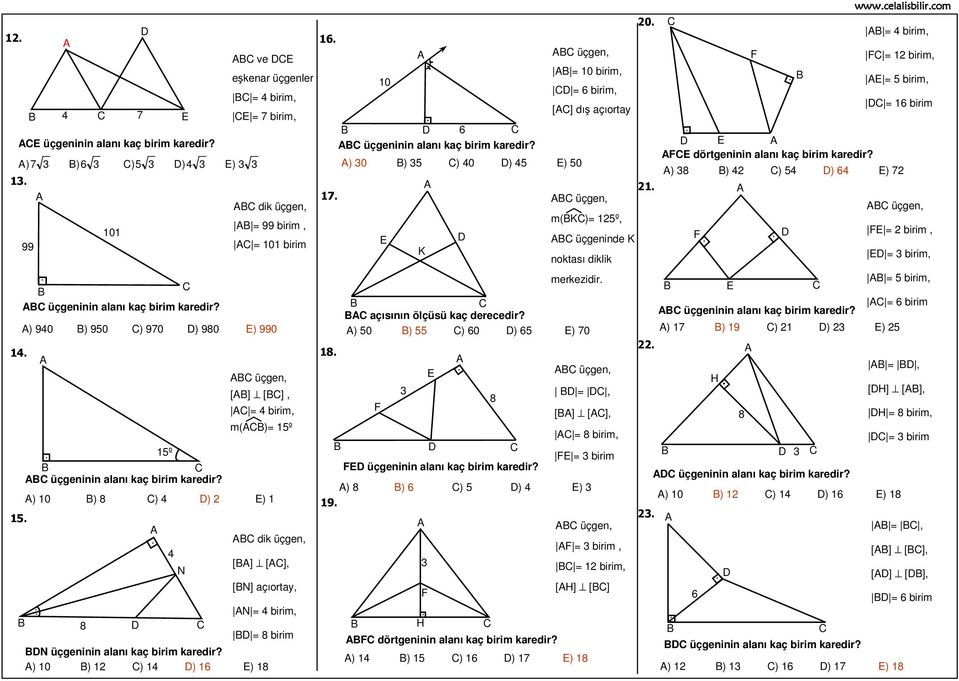



4 8 A D 2 Abc Ucgeninin Alani Kac Birim Karedir Abc Ucgeninin Alani Kac Birim Karedir A 16 B 18 C D 24 E º 135º Pdf Free Download




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Matematik Felsefesi Evde Egitim




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube



Dik Ucgen Vikipedi




15 75 90 Ucgeni Ozellikleri Ve Kurallari




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




Geometri 7 15 75 90 Ucgenleri Bolum 2 Youtube



15 75 90 Ucgeni Webders Net




Dik Ucgende Trigonometri Bikifi



最高 50 75 15 90 Ucgeninin Ozellikleri



Ab Ve Ac Yi Nasil Bulabilirim 150 Derecelik Ucgenin Alanini Sinus Teoremiyle Buldum Yardimci Olursaniz Cok Sevinirim Matematik Kafasi




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com




15 75 90 Ucgeni



2




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz



30 60 90 Ucgeni Ve Bagintilari Formulleri 8 Sinif Matematik 15 16




Dik Ucgen 15 75 90 Ucgeni Islemli Em Iyi Secicem Gereksiz Engellenir Eodev Com



Ozel Ucgenler Ppt Video Online Indir




Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri




Ikizkenar 15 75 90 Ucgeni Yardim Edebilir Misiniz Cozemedigim Sorular




Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri



15 75 90 Ucgeni




15 75 90 Ucgenin Ozelligi




135 30 15 Ucgenini Aciklayabilir Misiniz Eodev Com
.JPG)



Acilarina Gore Ucgen Cesitleri 4 9 Sinif Dik Ucgen Ve Trigonometrik Bagintilar Konu Anlatim Sunusu 19



Dik Ucgen Vikipedi



15 75 90 Ucgeni



15 75 90 Ucgeni Kenar Bagintisi Ispat




選択した画像 75 15 90 Ucgeni Kenarlari



15 75 90 Ucgeni Ozellikleri




15 75 90 Ucgeni Ve Dikdortgende Alan Youtube




Bir Ucgenin Cevresi Nasil Bulunur Wikihow



90 75 15 Ucgeni Ozellikleri




Dik Ucgende Trigonometri Bikifi
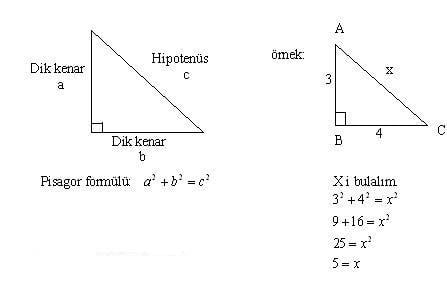



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com




15 75 90 Ucgeninin Ozelligi



Dik Ucgenin Alani Nasil Bulunur Dik Ucgenin Alani Nasil Hesaplanir Formulu Nedir Egitim Haberleri




Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri




15 75 90 Ucgeni Ozelliklerinin Ispati Ozeldersci



0 件のコメント:
コメントを投稿